本章会深入策略梯度算法，进一步学习 Natural Policy Gradient, Trust Region Policy Optimization, Proximal Policy Optimization等算法。

Policy Gradient as Policy Iteration

回顾Policy Gradient和Actor-Critic算法， $$ \nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \nabla_{\theta}\log \pi_{\theta}(a_{i, t} \vert s_{i, t}) A^{\pi}_{i, t} $$

可以看作一下过程

  1. 使用当前策略$\pi$估计$A^{\pi}_{i, t}$
  2. 基于$A^{\pi}(s_t, a_t)$来获得改进后的策略$\pi'$

与Policy Iteration过程相同。 什么情况下Policy Gradient可以看作Policy Iteration？首先我们分析Policy Gradient中的policy improvement。

策略梯度：

$$ J(\theta) = E_{\tau \sim p_{\theta}(\tau)}\left[ \sum_{t}\gamma^t r(s_t, a_t) \right] $$

新策略参数$\theta'$和旧策略参数$\theta$ 的policy improvement： $$ J(\theta') - J(\theta) = E_{\tau \sim p_{\theta'}(\tau)} \left[ \sum_t \gamma^t A^{\pi_{\theta}}(s_t, a_t) \right] $$ 旧策略$\theta$的advantage关于新策略$\theta'$的trajectory的期望值。

如果按照policy iteration的流程，在improvement中，也就只需要使得每步提升最大，找到新的parameter使得等式的右方最大化即可。但是improvement是计算新策略$\theta'$, 的轨迹期望，而我们当前的样本都是基于旧策略$\theta$采集的。

把improvement展开：

$$ E_{\tau \sim p_{\theta'}(\tau)} \left[ \sum_t \gamma^t A^{\pi_{\theta}}(s_t, a_t) \right] = \sum_t E_{s_{t} \sim p_{\theta'}(s_{t})} \left[ E_{a_{t} \sim \pi_{\theta'}(a_{t})} \left[ \gamma^t A^{\pi_{\theta}}(s_t, a_t) \right]\right] $$

然后使用Importance Sampling将动作从分布$\pi_{\theta'}(a_t)$转换到分布$\pi_{\theta}(a_t)$: $$ E_{\tau \sim p_{\theta'}(\tau)} \left[ \sum_t \gamma^t A^{\pi_{\theta}}(s_t, a_t) \right] = \sum_t E_{s_{t} \sim p_{\theta'}(s_{t})} \left[ E_{a_{t} \sim \pi_{\theta}(a_{t})} \left[ \frac{\pi_{\theta^{\prime}}(a_t)}{\pi_{\theta}(a_t)} \gamma^t A^{\pi_{\theta}}(s_t, a_t) \right]\right] $$

但是现在状态$s_t$仍然是来自于分布$p_{\theta'}$。 如果$\pi$和$\pi'$的**total variation divergence**（总变异散度，两个分布每个元素差值绝对值之和）小于$\epsilon$，

$$ \vert \pi_{\theta'}(a_t \vert s_t) - \pi_{\theta}(a_t \vert s_t) \vert \le \epsilon $$

那么$p_{\theta'}$和$p_{\theta}$的总变异散度有上界：

$$ \vert p_{\theta'}(s_t) - p_{\theta}(s_t) \vert \le 2\epsilon t $$

因而，improvement有上界

$$ J(\theta') - J(\theta) \le \sum_{t} 2\epsilon t C $$

其中$r_{max}$是最大单步奖励，$C \in O(\frac{r_{max}}{1 - \gamma})$。

最终，我们用$p_{\theta}$来替换 $p_{\theta'}$

$$ \begin{aligned} \overline{A}(\theta') &= \sum_t E_{s_t \sim p_{\theta}(s_t)}\left[ E_{a_t \sim \pi_{\theta}(a_t \vert s_t)}\left[ \frac{\pi_{\theta'}(a_t \vert s_t)}{\pi_{\theta}(a_t \vert s_t)} \gamma^t A^{\pi_{\theta}}(s_t, a_t) \right] \right]\\
\theta' &\leftarrow \arg\max_{\theta'} \overline{A}(\theta')
\end{aligned} $$

A better measure of divergence

在现实中，我们很难计算两个分布的total variation divergence，一般使用 KL Divergence替代。

实际上，两个分布$\pi_{\theta'}(a_t \vert s_t)$和 $\pi_{\theta}(a_t \vert s_t)$的total variation divergence上界可以用KL divergence($D_{KL}$)的均方根来表示。

$$ \vert \pi_{\theta'}(a_t \vert s_t) - \pi_{\theta}(a_t \vert s_t) \vert \le \sqrt{\frac{1}{2} D_{KL}\left(\pi_{\theta'}(a_t \vert s_t) \vert\vert \pi_{\theta}(a_t \vert s_t)\right)} $$

Enforcing the KL constraint

上文所有的证明都建立在$\pi'$和$\pi$之间的差异不大的基础上，因而需要有一个限制：

$$ D_{KL}\left(\pi_{\theta'(a_t \vert s_t)} \vert \vert \pi_{\theta}(a_t \vert s_t)\right) \le \epsilon $$

Dual Gradient Descent

拉格朗日乘子法与对偶问题

构造原优化问题的对偶问题，一方面减少了约束，另一方面对偶问题是凸优化问题，一定有最优解。

原始的优化目标在引入拉格朗日乘子后可以转化为如下的形式： $$ \label{eq:dual_opt} \mathcal{L}(\theta', \lambda) = \overline{A}(\theta') - \lambda \left(D_{KL}\left(\pi_{\theta'} (a_t \vert s_t) \vert\vert \pi_{\theta}(a_t \vert s_t)\right) - \epsilon\right) $$

基于dual gradient descent算法：

  1. 更新参数$\theta'$最大化$\mathcal{L}(\theta', \lambda)$（不必等到完全收敛，可以仅执行几步梯度更新）
  2. $\lambda \leftarrow \lambda + \alpha \left( D_{KL}\left(\pi_{\theta'}(a_t \vert s_t) \vert\vert \pi_{\theta}(a_t \vert s_t)\right) - \epsilon \right)$

乘子$\lambda$也是一个需要优化的参数。当约束违反程度大的时候，后面拉格朗日项就变成特别大的负项，如果需要最大化这个目标，则需要将乘子变大，反之依然。通过对这个乘子的调节，进而修正约束部分的重要性，从而达到自适应优化的目标。

Natural Gradients

除了将约束放进优化目标，另一个考虑的方向时修改目标函数。因为$\theta$和$\theta'$之间的差距很小，我们使用一阶泰勒展开在$\theta$处来近似$\theta'$。

即 $$ \begin{aligned} \theta' &\leftarrow \arg\max_{\theta'} \overline{A}(\theta') \\
\theta' &\leftarrow \arg\max_{\theta'}\nabla_\theta \overline{A}(\theta)^T(\theta'-\theta)
\end{aligned} $$

由 $$ \nabla_{\theta'}\overline{A}(\theta') = \sum_t E_{s_t \sim p_{\theta}(s_t)}\left[ E_{a_t \sim p_{\theta}(a_t \vert s_t)} \left[ {\pi_{\theta'}(s_t,a_t) \over \pi_\theta(s_t,a_t)} \gamma^t \nabla_{\theta'}\log\pi_{\theta'}(a_t \vert s_t) A^{\pi_{\theta}}(s_t, a_t) \right]\right] $$

得到 $$ \begin{aligned} \nabla_{\theta}\overline{A}(\theta) &= \sum_t E_{s_t \sim p_{\theta}(s_t)}\left[ E_{a_t \sim p_{\theta}(a_t \vert s_t)} \left[ {\pi_{\theta}(s_t,a_t) \over \pi_\theta(s_t,a_t)} \gamma^t \nabla_{\theta}\log\pi_{\theta}(a_t \vert s_t) A^{\pi_{\theta}}(s_t, a_t) \right]\right] \\
&= \sum_t E_{s_t \sim p_{\theta}(s_t)}\left[ E_{a_t \sim p_{\theta}(a_t \vert s_t)} \left[ \gamma^t \nabla_{\theta}\log\pi_{\theta}(a_t \vert s_t) A^{\pi_{\theta}}(s_t, a_t) \right]\right] \\
&= \nabla_\theta J(\theta) \end{aligned} $$

我们的优化目标： $$ \begin{aligned} \theta' \leftarrow \arg\max_{\theta'}\nabla_\theta J(\theta)^T(\theta'-\theta)\\
s.t. D_{KL}\left(\pi_{\theta'(a_t \vert s_t)} \vert \vert \pi_{\theta}(a_t \vert s_t)\right) \le \epsilon
\end{aligned} $$

对于gradient ascent来说， $$ \begin{aligned} \theta' \leftarrow \arg\max_{\theta'}\nabla_\theta J(\theta)^T(\theta'-\theta)\\
s.t. \vert\vert \theta' - \theta \vert\vert^2 \le \epsilon
\end{aligned} $$

Taking a Policy Gradient step means that we are taking a step in a circular radius around $\theta$, which is equivalent of maximizing $\overline{A}$ subject to $$ \vert\vert \theta' - \theta \vert\vert^2 \le \epsilon $$

natural gradients 使用二阶泰勒展开来近似KL Divergence：

$$ D_{KL}(\pi_{\theta'} \vert\vert \pi_{\theta}) \approx \frac{1}{2} (\theta' - \theta) \pmb{F} (\theta' - \theta) $$

其中$\pmb{F}$代表Fischer Information Matrix， 让我们的优化区域变成了一个椭圆。

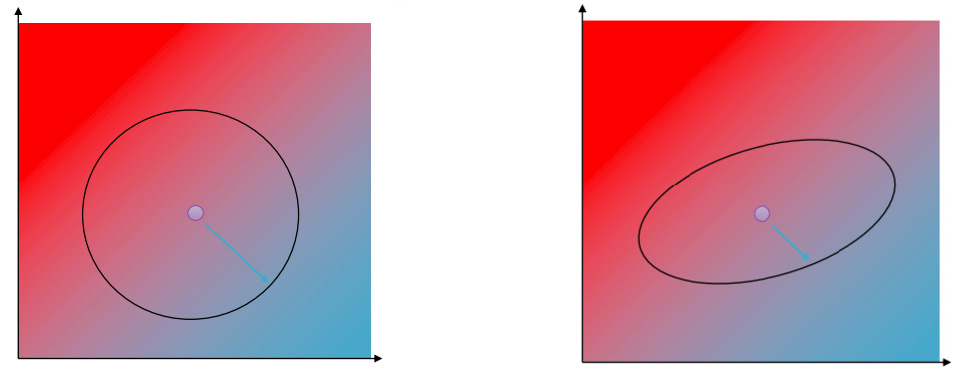上图是使用欧式距离约束（左）和使用近似KL散度约束的对比图。

We transform our objective by $\pmb{F}$ inverse, such that the optimiation region becomes again a circle and we can take a gradient step on this transformation. We call this the Natural Gradient:

$$ \theta' = \theta + \alpha \pmb{F}^{-1} \nabla_{\theta}J(\theta) $$ 学习率$\alpha$： $$ \alpha = \sqrt{\frac{2\epsilon}{\nabla_{\theta}J(\theta)^T\pmb{F}\nabla_{\theta}J(\theta)}} $$

更多Natural Gradients参考 J. Peters, S. Schaal, Reinforcement learning of motor skills with policy gradients。

Fischer Information Matrix定义为： $$ \pmb{F} = E_{\pi_{\theta}}\left[ \nabla_{\theta}\log\pi_{\theta}(\pmb{a}\vert\pmb{s}) \nabla_{\theta}\log\pi_{\theta}(\pmb{a}\vert\pmb{s})^T \right] $$

如果$\theta$具有一百万个参数，$\pmb{F}$就会是一百万乘上一百万的矩阵，对这个矩阵求逆显然不现实。

Trust Region Policy Optimization

Schulman et al., Trust Region Policy Optimization

TRPO主要针对NPG存在的两个问题提出了解决方案：第一个就是求逆矩阵的高复杂度问题，第二个则是对KL divergence做的approximation中可能存在的约束违反的问题做了预防。

首先就是求逆操作的高复杂度问题，TRPO将它转化为求解线性方程组，并利用conjugate gradient algorithm进行近似求解（这里有要求inverse matrix是positive definite的，所以在TRPO中有对目标函数的约束）。

而另外一点，如何对违反约束做限制，这里用的是exponential decay line search的方式，也就是对于一个样本，如果某次更新违反了约束，那么就把它的系数进行指数衰减，从而减少更新的幅度，直到它不再违反约束或者超过一定次数衰减则抛弃这次的数据。

Proximal Policy Optimization

Schulman et al., Proximal Policy Optimization, 提出了一种不要计算Fischer Information Matrix或者其近似值来满足$D_{KL}$限制的方法。

有两种方式：

  • Clipping the surrogate objective
  • Adaptive KL Penalty Coefficient

Clipping the surrogate objective

令$r(\theta)$为重要性采样权重，截断目标值为： $$ L^{CLIP} = E_t \left[ \min\left( r_r(\theta)A_t, clip(r_t(\theta), 1-\epsilon, 1+\epsilon)A_t \right) \right] $$

下图展示了$L^{CLIP}$在正的优势值和负优势值的情况。

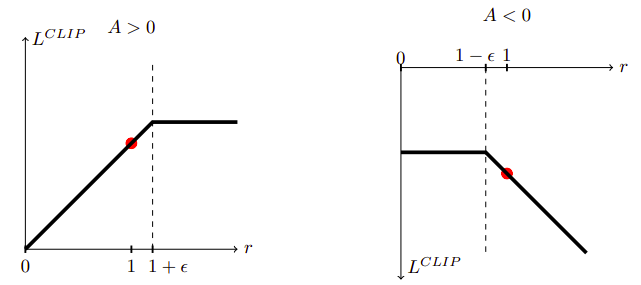
但最近的文章如Engstrom et al., Implementation Matters in Deep Policy Gradients 截断机制并没有阻止梯度步进破坏KL限制，提升点主要来自于 code-level optimizations，TRPO的表现其实更好。

Adaptive KL Penalty Coefficient

将KL散度作为惩罚项加入目标函数。 策略更新主要包含以下两步：

  • 使用minibatch SGD更新KL-penalized目标。

$ L^{KLPEN}(\theta) = E_t \left[ \frac{\pi_{\theta'}(a_t \vert s_t)}{\pi_{\theta}(a_t \vert s_t)} A^{\pi_{\theta}}(s_t, a_t) - \beta D_{KL}(\pi_{\theta'}(. \vert s_t)\vert\vert \pi_{\theta}(. \vert s_t)) \right] $

  • 计算$d = E_t \left[ D_{KL}(\pi_{\theta'}(. \vert s_t)\vert\vert \pi_{\theta}(. \vert s_t)) \right] $
    • If $d \lt d_{targ}/1.5$ then $\beta \leftarrow \beta/2$
    • If $d \gt 1.5 d_{targ}$ then $\beta \leftarrow 2\beta$

其中$d_{targ}$是期望KL Divergence目标值。