cs285 DRL notes lecture 8: Deep RL with Q-Functions
Contents
fitted q iteration与Q-Learning不同
- fitted q iteration算法:当前策略收集整个数据集,然后对Q函数进行多次回归近似,接下来收集新的数据集循环这一过程。
- Q-Learning(online q iteration):一边收集数据,一边进行学习。
Q-Learning的问题
Q-learning is not GD
Q-learning不是梯度下降,公式
$$
\begin{aligned}
y_i&=r(s_i,a_i)+\gamma max_{a'}Q_\phi(s_i',a_i')\\
\phi&\leftarrow \phi-\alpha{dQ_\phi\over d\phi}(s_i,a_i)(Q_\phi(s_i,a_i)-y_i)
\end{aligned}
$$
其中$y_i$与参数$\phi$相关,但没有梯度计算,因而不保证收敛。
one-step gradient
Q-Learning使用一个样本来更新梯度,更新非常不稳定,使用批次更新最优。
moving targets
目标值因为与神经网络参数相关,每次神经网络更新,目标值也会随之变动,严重影响收敛。
correlate samples
我们使用神经网路来近似Q函数,而神经网络学习数据一般要求独立同分布(i.i.d),但是在rl的采样中,序列决策问题的数据来源于与环境的相邻交互,数据之间往往是具有相关性的,即可能状态相似。神经网络会在局部状态过拟合,当学习新的状态时,遗忘旧的内容。
replay buffers
Replay Buffer是一个或者多个智能体采样得到样本的合集,会将所有样本都存储起来,直至容量上限。 当使用Q-Learning算法学习时,从其中随机拿出部分样本来进行神经网络训练。 Replay Buffer解决了上面提到的两个问题:one-step gradient和correlate samples。
使用Replay Buffer的Q-Learning算法如下
使用某种策略收集transition${(s_i,a_i,s'_i,r_i)}$并存储到replay buffer $\mathcal{B}$
For $K$ times
$\quad \text{获取样本批次}(s_i,a_i,s'_i,r_i)\leftarrow \mathcal{B}$
$\quad y_i\leftarrow r(s_i,a_i) + \gamma \max_{a'_i}Q_\phi(s'_i,a'_i)$
$\quad \phi \leftarrow \phi-\alpha\Sigma_i\frac{dQ_\phi}{d\phi}(s_i,a_i)(Q_\phi(s_i,a_i) - y_i)$
我们需要关心的是
- replay buffer的填充频率
- 存储transition的数量
- 采样的方式(均匀、权重等)
target network
我们希望目标值能够固定,一种方式是使用Q神经网络,固定其参数,用来计算目标值。目标网络会在神经网络更新后每隔一段时间进行更新,然后重复这一过程。

当N=1,K=1,是上述算法就成为了经典DQN算法。

为了避免Q函数和目标函数的lag变化过大,可以使用soft update $$\phi '=\tau\phi ' + (1-\tau)\phi \quad \ \tau=0.999$$
Double Q-Learning
Q-Learning算法存在overestimation问题,目标值 $$ y = r + \gamma \max_{a'}Q_{\phi'}(s', a') $$
对于$n$个随机变量$X_1$, .. $X_n$, $$ E\left[\max(X_1,\ …,\ X_n)\right] \ge max(E[X_1],\ …,\ E[X_n]) $$ 因此,当我们对目标值y取$\max$操作时,会不可避免高估Q值。 对于$Q_{\phi'}$的$\max$操作等同于 对取得最大$Q_{\phi'}$值的动作做$\arg\max$操作。
$$ \max_{a'}Q_{\phi'}(s', a') = Q_{\phi}(s', \arg\max_{a'}Q_{\phi'}(s', a')) $$
这个操作可以描述为两个过程,根据$Q_{\phi'}$去选择一个最佳的action,然后得到这个最佳action的Q值。over-estimation因为这个选到的aciton必然会导致得到的Q值最大。故而只要破坏这种相关性,这个问题就可以得到一定程度的解决.
Double Q-learning在这两个步骤中分别使用两个Q神经网络作为estimator,从而缓解这个问题。
$$ y = r + \gamma Q_{\phi'}(s', \arg\max_{a'}Q_{\phi}(s', a')) $$
选择action时对$Q_{\phi}$做$\arg\max$操作,然后基于$Q_{\phi'}$求对应的Q值。考虑到上文中已经提出对应的target network,可以仍然使用target network来估计Q值,选择动作时使用当前的网络$Q_{\phi}$。
Multi Step Returns
在actor-critic算法中,策略梯度目标值的计算有几种方式
$$
\begin{aligned}
Q&=\mathbb{E}[r_0+\gamma r_1+…+\gamma^{n}r_n]\quad\text{Monte-Carlo} \\
&=\mathbb{E}[r_0+\gamma V^\pi(s_1)]\quad \text{1 step TD} \\
&=\mathbb{E}[r_0+\gamma r_1+\gamma^2 V^\pi(s_2)]\quad \text{2 step TD} \\
&=\mathbb{E}[r_0+\gamma r_1+…+\gamma^{n}r_n+\gamma^n V^\pi(s_n)]\quad \text{n step TD} \\
\end{aligned}
$$
Monte-Carlo:无偏差,高方差; n-step returns:n越大,偏差越小,方差越大。
与之类似,我们构造Q-Learning的multi-step returns $$ y_t = \sum_{t'=t}^{t+N-1} \gamma^{t'-t} r_{t'} + \gamma^{N} \max_{a}Q_{\phi}(s_{t+N}, a) $$ 优缺点:
- 当Q值不准确的时候偏差更小
- 学习更快,尤其在前期(前期Q值估计不准确,targets中reward项占据主要部分)
- 只有on-policy(N=1)才正确
如何解决这个问题?
- 最常见的方法就是忽略它们,在现在大部分使用n-steps的算法,包括GORILA、Ape-X,R2D2等都是这样操作的。
- 另外则是可以利用某些手段去cut掉这些trace,一般都是通过两个policy生成这个trace的probability比值是否超过某个阈值来判定,比较著名的就是Retrace以及基于它的ACER,Reacotr,IMPALA等。
- 使用重要性采样。
Q Learning with Continuous Actions
连续动作空间在计算targets的时候会遇到问题,主要是关于动作的$\arg \max$操作无法实现。
Stochastic Optimization
一个简单有效的方法是采样$N$个动作$a_1$, …, $a_N$并选择Q值最大的动作: $$ \max_a Q_{\phi}(s, a) \approx max(Q_{\phi}(s, a_1),\ …,\ Q_{\phi}(s, a_N)) $$ 这种方法不是很准确,但速度快并且可以并行采样。
更准确的方法有:
- Cross Entropy Methods: 采集$N$个动作,利用最小化交叉熵来学习相应的策略分布,随着学习得到的策略越来越准确,得到的样本也越来越好。
- CMA-ES: 一种进化方法。
Easily Maximizable Q Functions
第二大类则是引入一些容易取max的Q-function。例如在NAF(Normalized Advantage Functions)中,将网络的输出分成三部分:
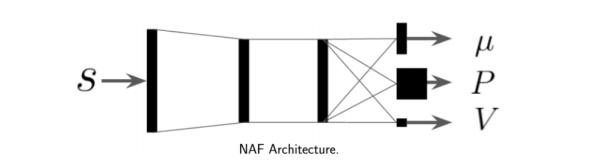
此时max操作和argmax操作都可以用其中的head来表示: $$ \arg\max_a Q_{\phi}(s, a) = \mu_{\phi}(s) $$ $$ \max_a Q_{\phi}(s, a) = V_{\phi}(s) $$ 而一般的Q值则是也可以通过它们组合得到:
$$ Q_{\phi}(s, a) = -\frac{1}{2}(a - \mu_{\phi}(s))^T P_{\phi}(s)(a - \mu_{\phi}(s)) + V_{\phi}(s) $$
这种方法的优点就是不对algorihtm本身作出改动,没有添加inner loop的计算量,效率保持一致。但是由于网络需要输出多个head,表达更多语意,会降低表达能力,需要更大网络。
DDPG (Deep Deterministic Policy Gradient)
训练另一个神经网络$\mu_{\theta}(s)$来近似$\arg\max_a Q_{\phi}(s, a)$。
$$ \theta \leftarrow \arg\max_{\theta} Q_{\phi}(s, \mu_{\theta}(s)) $$
$$ \frac{dQ_{\phi}}{d\theta} = \frac{da}{d\theta} \frac{dQ_{\phi}}{da} $$
DDPG 算法:

