本章学习基于值函数的强化学习方法。

隐式策略

尽管值函数方法忽略策略梯度，我们仍需要获得一个策略。

$$ \underset{a_t}{argmax}A^\pi(s_t,a_t) $$

表示在状态$s_t$和策略$\pi$下，$a_t$是最优的执行动作。至少优于任意$a\sim \pi(s_t,a_t)$，不管$\pi(s_t,a_t)$具体是什么。 那么，我们可以得到改进的策略为

$$ \pi^{'}(s_t,a_t)= \begin{cases} 1,\ & \text{if}\ a_t=\underset{a_t}{argmax}A^\pi(s_t,a_t)\\
0,\ & \text{otherwise} \end{cases} $$

策略$\pi^{'}$至少与策略$\pi$一样好，大多数情况下优于策略$\pi$。

策略更新

策略$\pi^{'}$优于$\pi$，我们可以不断更新策略，如图。

policy iteration

  1. 估计优势函数$A^\pi(s_t,a_t)$ #policy evaulation
  2. $\pi\leftarrow\pi^{'}$ //policy improvement

已知

$$ A^\pi(s_t,a_t)=r(s,a)+\gamma\mathbb{E}[V^\pi(s')]-V^\pi(s) $$

因此，我们可以通过估计值函数$V^\pi(s)$来更新策略。

动态规划

如果我们已知状态转移概率$p(s'|s,a)$并且状态$s$和动作$a$都是离散的，那么可以使用动态规划算法。

$$ V^\pi(s)\leftarrow \mathbb{E}_{a\sim\pi(a|s)} \left[r(s,a) + \gamma\mathbb{E}_{s'\sim p(s'|s,a)}\left[V^\pi(s')\right]\right] $$

因为策略是确定的，则期望值为常数，上式简化为

$$ V^\pi(s)\leftarrow r(s,\pi(s)) + \gamma\mathbb{E}_{s'\sim p(s'|s,a)}\left[V^\pi(s')\right] $$

policy iteration

  1. 估计值函数$V^\pi(s)\leftarrow r(s,\pi(s))+\gamma\mathbb{E}_{s'\sim p(s'|s,a)}\left[V^\pi(s')\right]$
  2. $\pi\leftarrow\pi^{'}$

策略迭代是首先创建/更新值函数表格，然后策略更新，直到策略收敛。

同时

$$ \arg max _{a_t}A^\pi(s,a) = \arg max _{a_t}Q^\pi(s,a) $$

因为二者只相差$V^\pi$，而这个值是与动作无关的。 $$Q^\pi(s,a) = r(s,a) + \gamma\mathbb{E}\left[V^\pi(s')\right]$$

因此，我们可以更新Q函数来得到最优策略。

value iteration

  1. $Q(s,a)\leftarrow r(s,a)+\gamma\mathbb{E}[V(s')]$
  2. $V(s)\leftarrow max_aQ(s,a)$

值迭代是首先创建Q函数表格，然后计算值函数（相当于策略更新），直到Q函数表格收敛。

最后得到最优策略 $$ \pi^*(s,a) = \arg max _{a}Q(s,a) $$

fitted value iteration

动态规划算法使用表格来记录值函数，当动作空间和状态空间过大时，难以适用，我们使用神经网络来近似值函数。

fitted value iteration

  1. $y_i\leftarrow max_{a_i}(r(s_i,a_i)+\gamma\mathbb{E}[V(s_i^{'})])$，仍然需要知道所有动作以及对应的奖励值
  2. $\phi\leftarrow \arg min_\phi{1\over2}\sum_i||V_\phi(s_i)-y_i||^2$

fitted q iteration

因为大多数情况下，我们并不知道环境的模型，因此无法进行value iteration。 我们能否借鉴policy-iteration到value-iteration的过程来实现Q iteration？ 参照fitted value iteration，首先是构建q值target。

$$y_i\leftarrow r(s_i,a_i)+\gamma\mathbb{E}[V(s_i^{'})]$$

这里关键是上式中的第二项，如何来做近似。

  • 当前策略下所有next state的值的期望：利用多次采样来近似
  • $V(s_i^{'})\leftarrow max_aQ(s_i^{'},a_i^{'})$

这样就得到fitted Q iteration

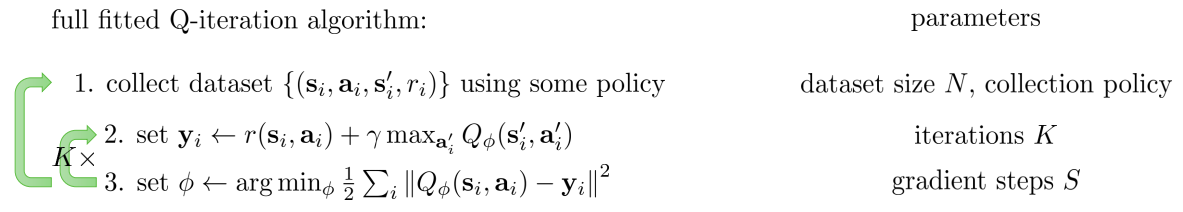
优缺点：

  • 可以使用off-policy样本。
  • 只有一个Q网络，方差低。
  • 不保证收敛。

Q iteration是off-policy的，因为学习用到的数据与策略$\pi$是无关的。

我们实际优化的目标值为$\epsilon$，定义为Bellman Error。

$$\epsilon = \frac{1}{2}\mathbb{E}_{(s,a)\sim\beta}\left[\left(Q_\phi(s,a) - \left[r(s,a)+\gamma\max_{a'}Q_\phi(s',a')\right]\right)^2\right]$$

当$\epsilon=0$，我们得到最优Q函数$Q^*$和最优策略$\pi^*$。

However, rather ironically, we do not know what we are optimizing in the previous steps, and this is a potential problem of the fitted Q-learning algorithm, and most convergence guarantees are lost when we do not have the tabular case.

online q iteration

online q iteration即一般意义上的Q-Learning算法。

  1. 执行动作$a_i$，得到transition$(s_i,a_i,s'_i,r_i)$
  2. $y_i = r(s_i,a_i) + \gamma \max_{a'}Q_\phi(s_i,a_i,s'_i,r_i)$
  3. $\phi \leftarrow \phi-\alpha\frac{dQ_\phi}{d\phi}(s_i,a_i)(Q_\phi(s_i,a_i) - y_i)$

exploration with Q-learning

如果只使用argmax策略，则缺少对环境的探索。

epsilon-greedy

$$ \pi(a_t|s_t)= \begin{cases} 1-\epsilon\ \text{if}\ a_t=\arg max_{a_t}Q_\phi(s_t,a_t)\\
\epsilon/({A}-1)\ \text{otherwise} \end{cases} $$

Boltzmann exploration

$$ \pi(a_t|s_t)\propto exp(Q_\phi(s_t,a_t)) $$