cs285 DRL notes lecture 6: Actor-Critic methods

回顾策略梯度算法， $$\nabla_\theta J(\theta) \simeq \frac{1}{N}\sum_{i=1}^N\left(\sum_{t=1}^T\nabla_\theta \log\pi_\theta(a_{i,t}|s_{i,t})\right)\left(\sum_{t'=t}^T r(s_{i,t'},a_{i,t'})\right)$$ 我们使用'‘reward-to-go’' 来近似在状态$s_{i,t}$采取动作 $a_{i,t}$的回报。上一章我们证明了这种近似具有很高的方差，这一章我们会使用其他方法来解决这个问题。

值函数作为基线

我们使用平均rewrad-to-go作为基线，定义为$\hat{Q}_{i,t}$表示在状态$s_{i,t}$采取动作$a_{i,t}$的期望奖励的估计，这一估计值并不准确。

而$Q(s_t, a_t) =\sum_{t'=t}^T{\mathbb{E}_{\pi_\theta}[r(s_t',a_t')|s_t]}$，代表reward-to-go的真实期望值，优于上式的近似表示。

$$\nabla_\theta J(\theta) \simeq \frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\nabla_{\theta}\log \pi_\theta (a_{i,t}|s_{i,t})Q(s_{i,t},a_{i,t})$$

同样baseline为$b_t = \frac{1}{N}\sum_i Q(s_{i,t},a_{i,t})$

$$\nabla_\theta J(\theta) \simeq \frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\nabla_{\theta}\log \pi_\theta (a_{i,t}|s_{i,t})(Q(s_{i,t},a_{i,t}) - b_t)$$

值函数$V^\pi(s_t)=\mathbb{E}_{a_t\sim \pi_\theta(a_t|s_t)}[Q^\pi(s_t,a_t)]$表示从状态$s_t$开始的期望总奖励。

优势函数$A^\pi(s_t,a_t)=Q^\pi(s_t,a_t)-V^\pi(s_t)$表示在状态$s_t$下采取动作$a_t$的好坏。

$$\nabla_\theta J(\theta) \simeq \frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\nabla_{\theta}\log \pi_\theta (a_{i,t}|s_{i,t})A^\pi(s_{i,t},a_{i,t})$$

值函数拟合

$Q^\pi,V^\pi,A^\pi$，我们需要拟合什么？ 其中，

$$ \begin{aligned} Q^\pi(s_t, a_t) &=r(s_t,a_t)+\sum_{t'=t+1}^T{\mathbb{E}_{\pi_\theta}[r(s_{t'},a_{t'})|s_t]}\\
&=r(s_t,a_t)+\mathbb{E}_{s_{t+1}\sim p(s_{t+1}|s_t,a_t)}[V^\pi(s_{t+1})]\\
&\simeq r(s_t,a_t)+V^\pi(s_{t+1})\\
A^\pi(s_t,a_t)&\simeq r(s_t,a_t)+V^\pi(s_{t+1}) - V^\pi(s_t) \end{aligned} $$

因此，我们只需要拟合$V^\pi(s_t)$。

策略评估

和策略梯度方法相似，我们可以使用蒙特卡洛方法来评估值函数$V^\pi(s_t)$。

$$ \begin{aligned} V^\pi(s_t) &= \sum_{t'=t}^T\mathbb{E}_{\pi_\theta}[r(s_{t'},a_{t'})|s_t]\\
&\simeq {1 \over N} \sum_{i=1}^N\sum_{t'=t}^Tr(s_{t'},a_{t'})|s_t\\
&\simeq \sum_{t'=t}^Tr(s_{t'},a_{t'})|s_t \end{aligned} $$

我们使用监督学习来拟合值函数，损失函数

$$ L(\phi)=1/2\sum_i||\hat{V}_\phi^\pi(s_i)-y_i||^2 $$

此处的$y_i$即为$V^\pi(s_i)$，$\hat{V}_\phi^\pi$是具有参数$\phi$的神经网络。

更进一步，使用bootstrap（自举）方法可以得到$y_i$

尽管上式对状态价值的估计是有偏的，但具有较低的方差。 最终的MSE损失形式为

$$ L(\phi)=1/2\sum_i||\hat{V}_\phi^\pi(s_i)-(r(s_{i,t}, a_{i,t})+\hat{V}_\phi^\pi(s_{i+1}))||^2 $$

从策略评估到actor-critic

batch actor-critic算法

1. 从策略$\pi_\theta(a|s)$采样${s_i, a_i}$
2. 使用采样得到的累计奖励来拟合$\hat{V}_\phi^\pi(s)$
3. 评估$\hat{A}^\pi(s_i,a_i)=r(s_i,a_i,s_{i+1})+\hat{V}_\phi^\pi(s_{i'})-\hat{V}_\phi^\pi(s_i)$
4. $\nabla_\theta J(\theta)\simeq \sum_i\nabla_\theta \log\pi_\theta(a_i|s_i)\hat{A}_\phi(s_i,a_i)$
5. $\theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$

折扣系数

当回合长度变的无穷大时，$\hat{V}_\phi^\pi$在许多情况下也会变的无穷大。这时我们使用折扣奖励来避免这种情况，另一方面的考虑是我们认为短期奖励要优于长期奖励。此时

$$ y_{i,t}\simeq r(s_{i,t},a_{i,t})+\gamma\hat{V}_\phi^\pi(s_{i,t+1}) $$

对于策略梯度使用折扣系数，这里有两种方式 $$\nabla_\theta J(\theta) \simeq \frac{1}{N}\sum_{i=1}^N\left(\sum_{t=1}^T\nabla_\theta \log\pi_\theta(a_{i,t}|s_{i,t})\right)\left(\sum_{t'=t}^T \gamma^{t'-t}r(s_{i,t'},a_{i,t'})\right)$$ 第二种： $$\begin{aligned} \nabla_\theta J(\theta) &\simeq \frac{1}{N}\sum_{i=1}^N\left(\sum_{t=1}^T\nabla_\theta \log\pi_\theta(a_{i,t}|s_{i,t})\right)\left(\sum_{t=1}^T \gamma^{t-1}r(s_{i,t},a_{i,t})\right)\\
&\simeq \frac{1}{N}\sum_{i=1}^N\left(\sum_{t=1}^T\nabla_\theta \log\pi_\theta(a_{i,t}|s_{i,t})\right)\left(\sum_{t'=t}^T \gamma^{t'-1}r(s_{i,t'},a_{i,t'})\right) ;\mathrm{(causality)}\\
&\simeq \frac{1}{N}\sum_{i=1}^N\left(\sum_{t=1}^T\gamma^{t-1}\nabla_\theta \log\pi_\theta(a_{i,t}|s_{i,t})\right)\left(\sum_{t'=t}^T \gamma^{t'-t}r(s_{i,t'},a_{i,t'})\right) \end{aligned}$$ 两种都是rewrad-to-go形式，一个是$\gamma^0, \gamma^1, \gamma^2…\gamma^{t'-t}$，而另一种系数则是$\gamma^{t-1}(\gamma^0, \gamma^1, \gamma^2…\gamma^{t'-t})$。 直观上，第二种方式采样时间靠后的样本梯度权重更小。实际中，我们采用第一种方式，这种方式的方差更小¹。

使用折扣系数的batch actor-critic算法

1. 从策略$\pi_\theta(a|s)$采样${s_i, a_i}$
2. 使用采样得到的累计奖励来拟合$\hat{V}_\phi^\pi(s)$
3. 评估$\hat{A}^\pi(s_i,a_i)=r(s_i,a_i,s_{i+1})+\gamma\hat{V}_\phi^\pi(s_{i'})-\hat{V}_\phi^\pi(s_i)$
4. $\nabla_\theta J(\theta)\simeq \sum_i\nabla_\theta \log\pi_\theta(a_i|s_i)\hat{A}_\phi(s_i,a_i)$
5. $\theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$

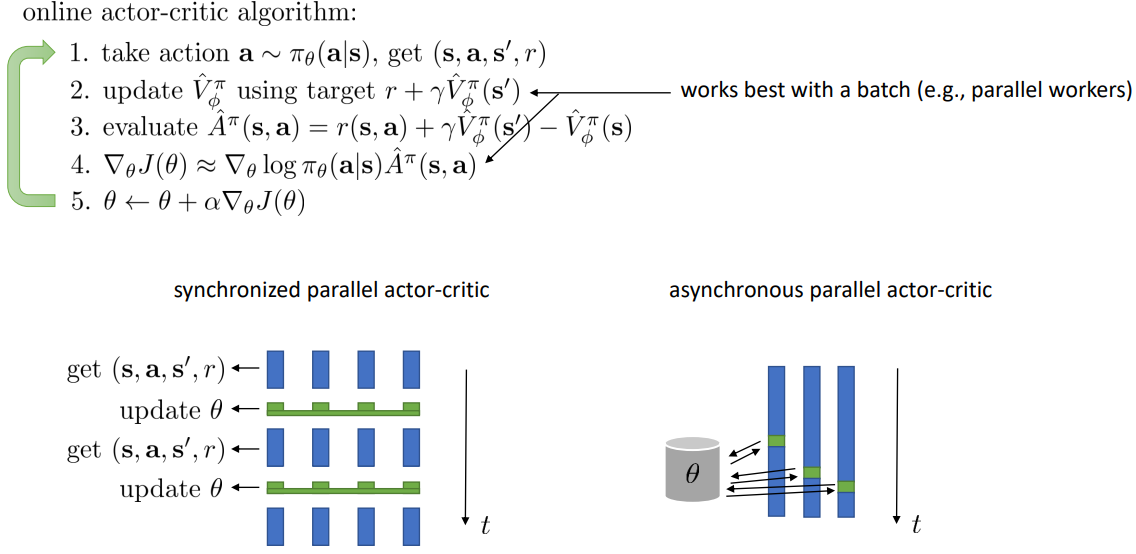
在线的actor-critic算法

1. 动作$a\sim\pi_\theta(a|s)$，得到transition采样${s, a,s',r}$
2. 使用target ${r+\gamma\hat{V}_\phi^\pi(s')}$来拟合$\hat{V}_\phi^\pi(s)$
3. 评估$\hat{A}^\pi(s,a)=r+\gamma\hat{V}_\phi^\pi(s')-\hat{V}_\phi^\pi(s)$
4. $\nabla_\theta J(\theta)\simeq \sum_i\nabla_\theta \log\pi_\theta(a|s)\hat{A}_\phi(s,a)$
5. $\theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$

actor-critic算法结构设计

使用两个神经网络分别来近似值函数和策略函数，优点：简单、有效，易于使用；缺点：在一些情况下，值函数和策略函数需要共享特征，特别在特征比较复杂时。

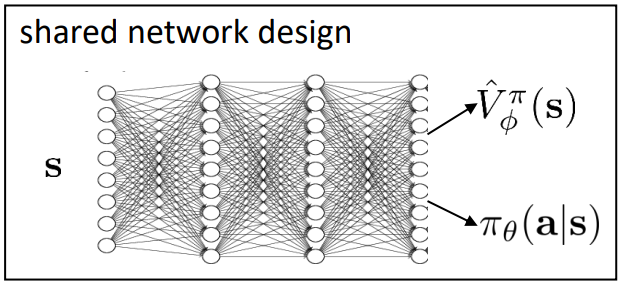
另一方面是使用并行的worker来批次更新效果会更好。值得注意的是，异步并行的actor-critic算法，行为策略会落后于学习策略，这回出现一些问题，具体在A3C算法中有描述。

critic作为baseline

actor-critic算法：有偏的，低方差

$$ \nabla_\theta J(\theta)\simeq {1 \over N}\sum_i^N\sum_t^T\nabla_\theta \log\pi_\theta(a_{i,t}|s_{i,t})(r(s_{i,t},a_{i,t},s_{i,t+1})+\gamma\hat{V}_\phi^\pi(s_{i,t+1})-\hat{V}_\phi^\pi(s_{i,t})) $$

策略梯度算法：无偏，高方差

$$ \nabla_\theta J(\theta)\simeq {1 \over N}\sum_i^N\sum_t^T\nabla_\theta \log\pi_\theta(a_{i,t}|s_{i,t})((\sum_{t'=t}^T\gamma^{t'-t} r(s_{i,t'},a_{i,t'})) - b) $$

state-dependent baseline：无偏，较低方差

$$ \nabla_\theta J(\theta)\simeq {1 \over N}\sum_i^N\sum_t^T\nabla_\theta \log\pi_\theta(a_{i,t}|s_{i,t})((\sum_{t'=t}^T\gamma^{t'-t} r(s_{i,t'},a_{i,t'})) - \hat{V}_\phi^\pi(s_{i,t})) $$

control variate: action dependent baseline

控制变量法（英语：control variates）是在蒙特卡洛方法中用于减少方差的一种技术方法。该方法通过对已知量的了解来减少对未知量估计的误差。

强化学习中，QProp算法采用了control variate的思想，在无偏的情况下来减少策略梯度中的方差。

Eligibility traces & n-step returns

eligibility trace称为资格迹，最先在$TD(\lambda)$中使用。$e_t$表示第t步资格迹，是值函数的优化微分值。 其优化的技术称为(backward view)。仔细观察公式可以发现$e_t$的算法中包含了以前的微分值，考虑了过去的价值梯度对更新参数$\theta$的影响。

$$ \begin{aligned} e_0&\doteq 0\\
e_t&\doteq \nabla\hat{V}_{\theta}(s_t) + \lambda\gamma e_{t-1}\\
\theta &\leftarrow \theta + \alpha (r_{t+1}+\gamma\hat{V}_{\theta}(s_{t+1})-\hat{V}_{\theta}(s_t))e_t
\end{aligned} $$

对比两种方法计算的策略梯度：

• Monte-Carlo方法：无偏，高方差。
• actor-critic方法：有偏，低方差。

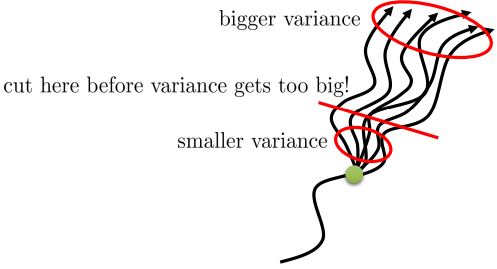
我们希望结合这两种方法，使用Monte-Carlo方法来计算近期的值估计，使用actor-critic方法来计算将来的值估计。结合下图，我们希望在方差变的过大之前截断轨迹，只使用 n步数据。

$$ \begin{aligned} Q&=\mathbb{E}[r_0+\gamma r_1+…+\gamma^{n}r_n]\quad\text{Monte-Carlo} \\
&=\mathbb{E}[r_0+\gamma V^\pi(s_1)]\quad \text{1 step TD} \\
&=\mathbb{E}[r_0+\gamma r_1+\gamma^2 V^\pi(s_2)]\quad \text{2 step TD} \\
&=\mathbb{E}[r_0+\gamma r_1+…+\gamma^{n}r_n+\gamma^n V^\pi(s_n)]\quad \text{n step TD} \\
\end{aligned} $$

n-step优势函数为：

GAE

GAE(Generalized Advantage Estimator，通用优势估计)。

上一小节我们介绍了n-step return，但我们不一定只能选择一个n，可以将所有n对应优势估计进行加权求和。

权重的选择是

由

$$ \begin{aligned} \hat{A}_1^\pi(s_t,a_t)&=\delta_t=r(s_{t},a_{t})+\gamma^1\hat{V}_\phi^\pi(s_{t+1})-\hat{V}_\phi^\pi(s_t)\\
\hat{A}_2^\pi(s_t,a_t)&=r(s_t,a_t)+\gamma r(s_{t+1},a_{t+1})+\gamma^2\hat{V}_\phi^\pi(s_{t+2})-\hat{V}_\phi^\pi(s_{t+1})\\
&=\delta_t+\gamma\delta_{t+1}\\
\hat{A}_n^\pi(s_t,a_t)&=\sum_{i=0}^{n-1}\gamma^i\delta_{t+i}\\
\end{aligned} $$

因此，

当$\lambda=0$时，$\hat{A}_{GAE}^\pi=\delta_t$，即TD Error。

当$\lambda=1$时，$\hat{A}_{GAE}^\pi=\sum_{i=0}^{\infty}\delta_{t+i}\gamma^i=\sum_{i=0}^{\infty}r_{t+i}\gamma^i - V(s_t)$，即Monte-Carlo Advantage。

初始化gae=0
$\delta=r_t+\gamma V(s_{t+1})m_t-V(s_t)$
更新gae $gae_t=\delta + \gamma\ast\lambda \ast m_t\ast gae_{t+1}$
计算returns $R_t(s_t,a_t)=gae_t+V(s_t)$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def get_advantages(values, masks, rewards):
    """
    masks: 表示回合是否结束
    """
    returns = []
    gae = 0
    for i in reversed(range(len(rewards))):
        delta = rewards[i] + gamma * values[i + 1] * masks[i] - values[i]
        gae = delta + gamma * lmbda * masks[i] * gae
        returns.append(gae + values[i])
    returns = list(reversed(returns))
    adv = np.array(returns) - values[:-1]
    return returns, (adv - np.mean(adv)) / (np.std(adv) + 1e-10)