强化学习是一种目标导向的学习方法，通过不断试错，奖励或惩罚智能体从而使其未来更容易重复或者放弃某一动作。

强化学习中的术语介绍。

强化学习的主要角色是智能体和环境，环境是智能体存在和互动的世界。智能体在每一步的交互中，如图所示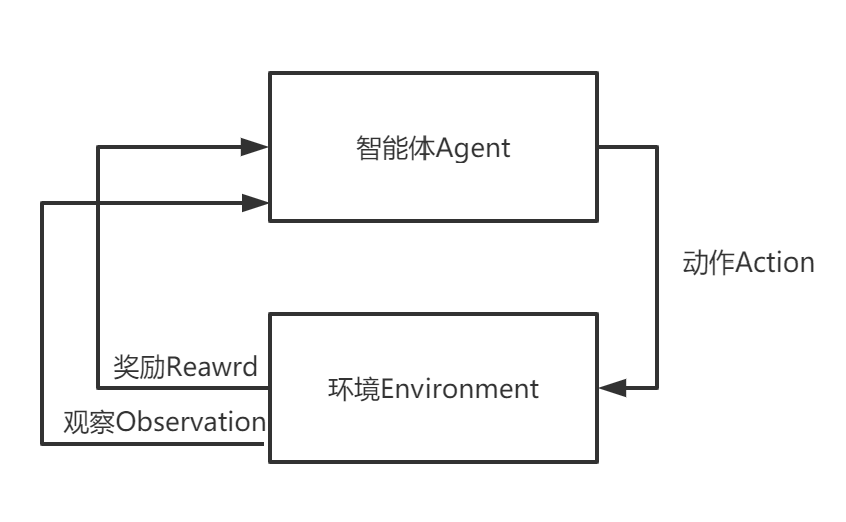， RL diagram 都会获得对于所处环境状态的观察（可能只是部分环境状态）， 然后决定下一步要执行的动作。环境的状态会在智能体执行动作后发生变化，但也可能会自行发生改变。 智能体还感知来自环境的奖励信号，奖励信号告诉了智能体当前环境状态的好坏。智能体的目标是最大化其累积奖励，称为回报(return)。

在$t$时刻, 定义系统的状态为$s_t$。 系统的状态可以是系统本身的属性。 定义智能体的动作为$a_t$。策略{policy}是一个从状态到动作的映射，是一种决策规则。

策略分为确定性策略$a_t=\pi_\theta(s_t)$或者随机性策略（策略输出动作分布） $\pi_\theta(a_t|s_t)$。很多情形下，状态不是完全可观测的{fully observable}，因此智能体智能观察到部分（partially observe）状态$o_t$。此时策略建立在$o_t$之上。

定义环境状态转移概率{transition function}为系统模型。状态转移函数一般是随机的，表现为一定分布特征，定义为$p(s_{t+1}|s_t, a_t)$。状态转移函数表示在时间$t$的动作和状态，转移到下一个状态的概率。一系列连续的动作和状态组成了一条轨迹{trajectory}=$\tau$。

定义奖励函数{reward function}=$r(s,a)$，表示在当前状态下执行动作获得的奖励。 奖励函数需要人工设计或者逆强化学习学习得到。

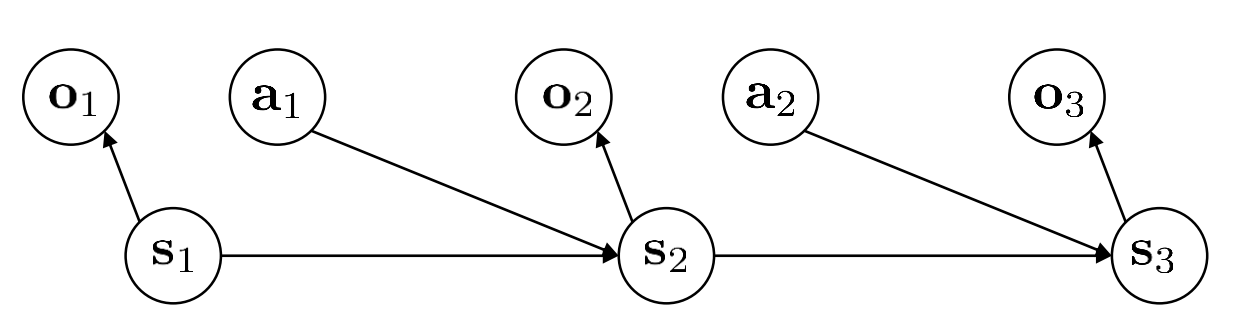
在大部分强化学习环境中，认为状态转换具有马尔可夫性质{Markovian}，即在$t+1$时刻的状态只依赖于$t$时刻的状态。 如图解释了马尔可夫链，箭头代表着因果关系。 Markov Chain

强化学习的目标是最大化累计奖励值。定义轨迹概率分布为$p_\theta(\tau)$，根据贝叶斯定理： $$ p(\tau)= p(s_1,a_1,…,s_T,a_T) = p(s_1)\prod_{t=1}^T\pi_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t)$$ 其中，$T$是回合的长度。

根据上式，可以计算出轨迹累计奖励期望值为

$$\mathbb{E}_{\tau\sim p_\theta(\tau)}\left[\sum_t r(s_t,a_t)\right]$$

为了最大化累计奖励期望值，需要优化$\theta$，直到得到$\theta$满足下式：

$$ \theta = \underset{\theta}{argmax}\mathbb{E}_{\tau\sim p_\theta(\tau)}\left[\sum_t r(s_t,a_t)\right] $$

状态值函数和Q函数

为了简化形式，引入两个函数。状态动作价值函数即Q函数和状态价值函数V。在DRL中，这两个函数一般是需要使用神经网络建模的对象。

Q函数

Q函数记为$Q(s_t,a_t)$，衡量在状态$s_t$下采取动作$a_t$的价值。 具体计算：从当前时刻状态$s_t$和动作$a_t$开始的奖励值的期望。 $$Q^\pi(s_t,a_t) = \sum_{t'=t}^T{\mathbb{E}_{\pi_\theta}[r(s_t',a_t')|s_t,a_t]}$$

状态值函数

状态值函数衡量状态$s_t$的价值。定义为$V^\pi(s_t) =\sum_{t'=t}^T{\mathbb{E}_{\pi_\theta}[r(s_t',a_t')|s_t]}$。

同样根据贝叶斯定理，状态值函数与Q函数的关系为： $V^\pi(s_t)=\mathbb{E}_{a_t\sim\pi(a_t|s_t)}[Q^\pi(s_t,a_t)]$.

更近一步，如果将初始状态的所有可能状态值相加，就可以得到强化学习的目标值。 $\mathbb{E}_{s_1\sim p(s_1)}[V^\pi(s_1)]$，其中$p(s_1)$代表所有可能的初始状态。

Reinforcement Learning Anatomy

如图，强化学习过程主要分为3个步骤：1）生成数据：根据不同的算法可以使用各种策略与环境交互；2）估计回报或者拟合环境模型（model based）；3）改进当前策略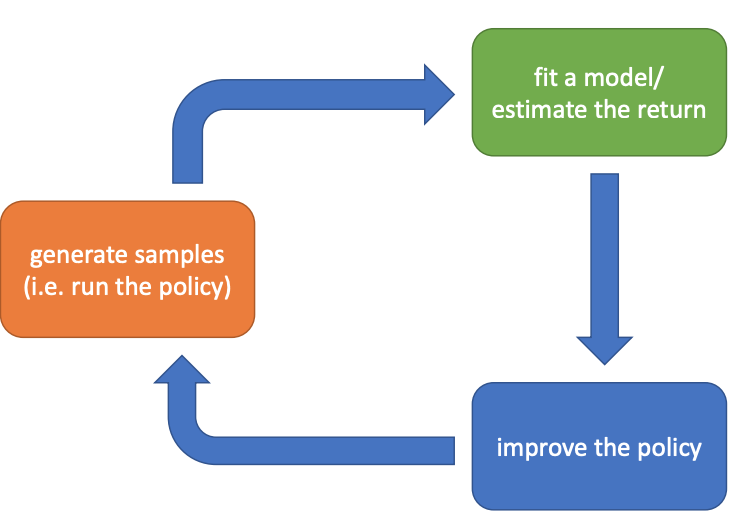； RL anatomy 强化学习的关键就在于正确高效地完成这三个步骤。