model-free强化学习忽略了状态转移概率$p(s_{t+1}|s_t,a_t)$，因为实际情况环境的模型往往无法获得或者学习。但也有一些例外：

模型已知

  1. 游戏(e.g., Atari games, chess, Go)
  2. 模型简单系统
  3. 仿真环境(e.g., 仿真机器人)

模型可以学习

  1. 系统识别（学习已知系统模型的参数）
  2. 利用观察得到的transition数据来学习特定的模型

open-loop vs closed-loop

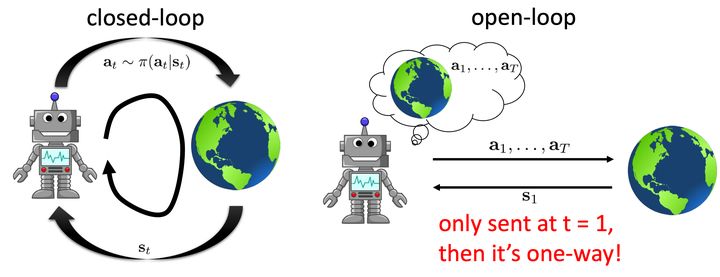
  • open-loop：只在t=1时，给与智能体初始状态$s_1$，之后智能体根据模型规划处一系列动作。
  • closed-loop：智能体会与环境不断交互，一般意义上的RL。

Deterministic environments:

给定初始状态$s_1$，然后就可以根据模型执行一系列动作${a_1, …, a_T}$，我们希望根据这些动作得到的轨迹奖励最大：

$$ a_1, …, a_T = \arg \max_{a_1, …, a_T} \sum_t r(s_t, a_t) \space \space \space \space s.t. \space s_{t+1} = \mathcal{T} (s_t, a_t) $$

Stochastic environment open-loop:

对于随机环境，我们可以得到轨迹概率：

$$ p_\theta(s_1, …, s_T \mid a_1, …, a_T) = p(s_1) \prod_t p(s_{t+1} \mid s_t, a_t) $$

目标是最大化期望轨迹奖励：

$$ a_1, …, a_T = \arg \max_{a_1, …, a_T} E \left[ \sum_t r(s_t, a_t) \mid a_1, …, a_T \right] $$

Stochastic environment closed-loop:

在closed-loop中，我们需要一个策略$\pi$来根据环境的反馈来做决策：

$$ \pi = \arg \max_{\pi} E_{\tau \sim p(\tau)} \left[ \sum_t r(s_t, a_t) \right] $$

Open-Loop planning

${a_1, …, a_T}$写作$A$，回报为$J$，我们优化的目标是：

$$ A = \arg \max_A J(A) $$

Stochastic optimization methods

Black-box优化方法。

Guess & Check (Random Search)

Algorithm:

  1. 从一个分布$p(A)$ (e.g. uniform)采样得到$A_1,…, A_N$
  2. 依据$\arg \max_i J(A_i)$选择$A_i$

样本越多，结果越准确。

Cross-Entropy Method (CEM)

CEM方法采用回报高的轨迹进行训练，提高对应动作发生概率，在不断接近最优策略的同时， 样本的质量也随之提高。

Algorithm:

  1. 从一个分布$p(A)$（Gaussian distribution）采样得到$A_1,…, A_N$
  2. 选择$M$个奖励最大的$A^1,…,A^M$ elites samples
  3. 使用$A^1,…,A^M$来近似$p(A)$

特点：

  • 易于实现和并行化
  • 对于低维系统（小于64）和短的time-horizon任务表现较好

Improvements: CMA-ES, implements momentum into CEM.

Monte Carlo Tree Search (MCTS)

如果把MDP看做一棵树（节点代表状态，边代表动作），那么我们可以将discrete planning问题转化为搜索问题，即遍历这棵树找到每个状态的价值，进而得到最优的策略。

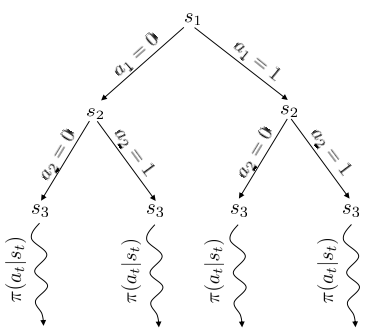
然而，随着动作空间增大，节点的数量以指数级递增，完全遍历无法实现。 因此，MCTS提出有选择地遍历，即对树进行剪枝。MTCS就是基于对叶节点的好坏评估以及探索次数的平衡做的剪枝。

MCTS Algorithm:

TreePolicy：来到一个状态$s_t$后如何选择哪一个分支做拓展。 DefaultPolicy：探索时的行为策略。

一般TreePolicy: UCT (Upper Confidence bounds applied to Trees):

  • 如果$s_t$没有完全探索，选择一个新动作$a_t$。
  • 否则，选择$Score(s_t)$最大的子节点。

$Score(s_t)$计算如下： $$ Score(s_t) = \frac{Q(s_t)}{N(s_t)} + 2C\sqrt{\frac{2\log N(s_{t-1})}{N(s_{t-1})}} $$

其中$Q(s_t)$代表状态的"Quality"，$N(s_t)$代表被访问过的次数，$C$表示我们对于较少访问到的节点的偏重。

更多资料：

  • MCTS-survey here
  • 在DAgger中替代手工标注paper

Trajectory optimization

**IDEA:**将问题表示为控制问题($x_t$代表状态，$u_t$代表动作，$c$代表cost)，然后我们来求解具有约束的优化问题：

$$ min_{u_1,…u_T} \sum_t c(x_t, u_t) \space \space \space \space s.t. \space x_t=f(x_{t_1}, u_{t-1}) $$

Collocation method

同时优化actions和states，具有约束。

$$ min_{u_1,…u_T, x_1,…,x_T} \sum_t c(x_t, u_t) \space \space \space \space s.t. \space x_t=f(x_{t_1}, u_{t-1}) $$

Shooting method

IDEA: 通过替换$f$将有约束问题转化为无约束问题，只针对action进行优化${u_1,…,u_T}$：

$$ min_{u_1,…u_T} \sum_t c(x_1, u_1) + c(f(x_1, u_1), u_2) + … + c(f(f(…)), u_T) $$

If open-loop, deterministic env, linear $f$, quadratic $c$:

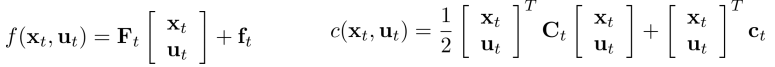
Linear Quadratic Regulator (LQR): 建立二阶导数矩阵(Hessian)代价太大，LQR选择逐步解决这个问题：

If open-loop, stochastic env, linear $f$, quadratic $c$:

选择高斯分布作为dynamics：$x_{t+1} \sim \mathcal{N} \left( F_t \begin{vmatrix} x_t,\
u_t \end{vmatrix} + f_t, \Sigma_t\right)$, the exact same algorithm will yield the optimal result.

动作为$K_t s_t + k_t$

Non-linear case:

使用iterative LQR (iLQR)或者Differential Dynamic Programming (DDP)。

等价于Newton法，具体见paper.